- S -> S + A | S – A | A + S | A – S | B*A
B -> aB | B(a+B) | a(a+B) | B*a|b
A -> a
S -> A+SS’ | A – S S’ | B*AS’
S’ -> +AS’ | -AS’ | Ɛ
S -> AS’‘| B*AS’
S’’ -> +SS’ | -SS’
B -> aBB’ | a(a+B)B’ | bB’
B’ -> (a+B)B’ | *aB’ |Ɛ
B -> aB’’ | bB’
B’’ -> BB’ | (a+B)B’
A -> a
State Yang Digunakan
S -> AS’‘| B*AS’
S’ -> +AS’ | -AS’ | Ɛ
S’’ -> +SS’ | -SS’
B -> aB’’ | bB’
B’ -> (a+B)B’ |*aB’| Ɛ
B’’ -> BB’ | (a+B)B’
A -> a
First S ={a,b}
First S’ ={+,-, Ɛ }
First S’’ ={+,-}
First B ={a,b}
First B’ ={(,*, Ɛ }
First B’’ ={a,b,(}
First A ={a}
Follow S= {$}
Follow S’= {$}
Follow S’’= {$}
Follow B= {*,)}
Follow B’= {*,)}
Follow B’’= {*.)}
Follow A= {+,-,$}
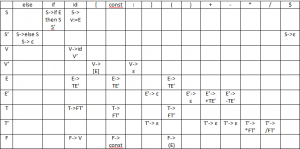
| + | – | * | ( | ) | a | b | $ | |
| S | S -> AS’S -> B*AS’’ | S -> B*AS’ | ||||||
| S’ | S’ -> +AS’ | S’ -> -AS’ | S’ -> Ɛ | |||||
| S’’ | S’’ -> +SS’ | S’’ -> -SS’ | ||||||
| B | B -> aB’’ | B -> bB’ | ||||||
| B’ | B’ -> *aB’B’ -> Ɛ | B’ -> (a+B)B’ | B’ -> Ɛ | |||||
| B’’ | B’’ -> (a+B)B’ | B’’ -> BB’ | B’’ -> BB’ | |||||
| A | A -> a |
Soal 2 :
S-> if E then S |if E then S else S | V:=E
V-> id | id [E]
E-> E+T | E-T | T
T-> T*F | T/F | F
F-> V | (E) | const
Jawab :
S-> if E then S S’ | V:=E
S’-> ε | else S
V -> id V’
V’-> ε |[E]
E-> TE’
E’-> +TE’ | -TE’ | ε
T-> FT’
T’-> *FT’ | /FT’ | ε
F-> V | (E) | const
First (S) = {if, id}
First (S’) = {ε,else}
First (V) = {id}
First (V’) = {ε,[}
First (E) = {id,(,const}
First (E’) = {+,-,ε}
First (T) = {id,(,const}
First (T’) = {*,/,ε}
First (F) = {id,(,const}
Follow (S) = {$,else}
Follow (S’) = {$,else}
Follow (V) = {:}
Follow (V’) = {:}
Follow (E) = {],)}
Follow (E’) = {],)}
Follow (T) = {+,-,]}
Follow (T’) = {+,-,]}
Follow (F) = {*,/,+,-,],}
No. 3
S -> a = A
A ->aA’ | bA’
A’ -> +AA’ | Ɛ
Tentukan First dan Follow dari
Jawab
First S = {a}
First A = {a,b}
First A’ = { +,Ɛ}
Follow S = { $ }
Follow A = { $, + }
Follow A’ = { $, + }
Parsing Table
|
NONTERMINAL |
INPUT SYMBOL |
|||
|
a |
b |
+ |
$ |
|
|
S |
S-> a=A |
|||
|
A |
A-> aA’ |
A->bA’ |
||
|
A’ |
A’ ->+AA’ A’ ->Ɛ |
A’ ->Ɛ |
||
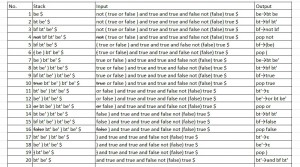
4.
First (be) = not, (, true, false
First(be’)= or, ε
First(bt)= not, (, true, false
First(bt’)= and, ε
First(bf)= not, (, true, false
Follow (be) = {$,)}
Follow(be’)= {$,)}
Follow(bt)= {or,$,)}
Follow(bt’)= {or,$,)}
Follow(bf)= {or,$,), and}